Richards Equation
3.1Introduction¶
Studying the processes that occur in the vadose zone, the region between the earth's surface and the fully saturated zone, is of critical importance for understanding our groundwater resources. Fluid flow in the vadose zone is described by the Richards equation and parameterized by hydraulic conductivity, which is a nonlinear function of pressure head Richards, 1931Celia et al., 1990. Typically, hydraulic conductivity is heterogeneous and can have a large dynamic range. In any site characterization, the spatial estimation of the hydraulic conductivity function is an important step. Achieving this, however, requires the ability to efficiently solve and optimize the nonlinear, time-domain Richards equation. Rather than working with a full, implicit, 3D time-domain system of equations, simplifications are consistently used to avert the conceptual, practical, and computational difficulties inherent in the parameterization and inversion of the Richards equation. These simplifications typically parameterize the conductivity and assume that it is a simple function in space, often adopting a homogeneous or one dimensional layered soil profile (cf. Binley et al., 2002Deiana et al., 2007Hinnell et al., 2010Liang & Uchida, 2014). Due to the lack of constraining hydrologic data, such assumptions are often satisfactory for fitting observed measurements, especially in two and three dimensions as well as in time. However, as more data become available, through spatially extensive surveys and time-lapse proxy measurements (e.g. direct current resistivity surveys and distributed temperature sensing), extracting more information about subsurface hydrogeologic parameters becomes a possibility. The proxy data can be directly incorporated through an empirical relation (e.g. Archie, 1942) or time-lapse estimations can be structurally incorporated through some sort of regularization technique Haber & Gazit, 2013Haber & Oldenburg, 1997Hinnell et al., 2010. Recent advances have been made for the forward simulation of the Richards equation in a computationally-scalable manner Orgogozo et al., 2014. However, the inverse problem is non-trivial, especially in three-dimensions Towara et al., 2015, and must be considered using modern numerical techniques that allow for spatial estimation of hydraulic parameters. However, this is especially intricate to both derive and implement due to the nonlinear, time-dependent forward simulation and potential model dependence in many aspects of the Richards equation (e.g. multiple empirical relations, boundary/initial conditions). To our knowledge, there has been no large-scale inversion for distributed hydraulic parameters in three dimensions using the Richards equation as the forward simulation.
Inverse problems in space and time are often referred to as history matching problems (see Oliver & Chen (2011)Dean et al. (2008)Sarma et al. (2007)Oliver & Reynolds (2001)Šimunek & Senja (2012) and reference within). Inversions use a flow simulation model, combined with some a-priori information, in order to estimate a spatially variable hydraulic conductivity function that approximately yields the observed data. The literature shows a variety of approaches for this inverse problem, including trial-and-error, stochastic methods, and various gradient based methods Bitterlich et al., 2004Binley et al., 2002Carrick et al., 2010Durner, 1994Finsterle & Zhang, 2011Mualem, 1976Šimunek & Genuchten, 1996. The way in which the computational complexity of the inverse method scales becomes important as problem size increases Towara et al., 2015. Computational memory and time often become a bottleneck for solving the inverse problem, both when the problem is solved in 2D and, particularly, when it is solved in 3D Haber et al., 2000. To solve the inverse problem, stochastic methods are often employed, which have an advantage in that they can examine the full parameter space and give insights into non-uniqueness Finsterle & Kowalsky, 2011. However, as the number of parameters we seek to recover in an inversion increases, these stochastic methods require that the forward problem be solved many times, which often makes these methods impractical. This scalability, especially in the context of hydrogeophysics has been explicitly noted in the literature (cf. Binley et al. (2002)Deiana et al. (2007)Towara et al. (2015)Linde & Doetsch (2016)).
Derivative-based optimization techniques become a practical alternative when the forward problem is computationally expensive or when there are many parameters to estimate (i.e. thousands to millions). Inverse problems are ill-posed and thus to pose a solvable optimization problem, an appropriate regularization is combined with a measure of the data misfit to state a deterministic optimization problem Tikhonov & Arsenin, 1977. Alternatively, if prior information can be formulated using a statistical framework, we can use Bayesian techniques to obtain an estimator through the Maximum A Posteriori model (MAP) Kaipio & Somersalo, 2004. In the context of Bayesian estimation, gradient based methods are also important, as they can be used to efficiently sample the posterior Bui-Thanh & Ghattas, 2015.
A number of authors have sought solutions for the inverse problem, where the forward problem is the Richards equation (cf. Bitterlich & Knabner, 2002Iden & Durner, 2007Šimunek & Senja, 2012 and references within). The discretization of the Richards equation is commonly completed by an implicit method in time and a finite volume or finite element method in space. Most work uses a Newton-like method for the resulting nonlinear system, which arises from the discretization of the forward problem. For the deterministic inverse problem using the Richards equation, previous work uses some version of a Gauss-Newton method (e.g. Levenberg-Marquardt), with a direct calculation of the sensitivity matrix Finsterle & Kowalsky, 2011Šimunek & Genuchten, 1996Bitterlich & Knabner, 2002. However, while these approaches allow for inversions of moderate scale, they have one major drawback: the sensitivity matrix is large and dense; its computation requires dense linear algebra and a non-trivial amount of memory (cf. Towara et al., 2015). Previous work used either external numerical differentiation (e.g. PEST) or automatic differentiation in order to directly compute the sensitivity matrix Finsterle & Zhang, 2011Bitterlich & Knabner, 2002Doherty, 2004Towara et al., 2015. Finite difference can generate inaccuracies in the sensitivity matrix and, consequently, tarry the convergence of the optimization algorithm. Furthermore, external numerical differentiation is computationally intensive and limits the number of model parameters that can be estimated.
The goal of this chapter is to suggest a modern numerical formulation that allows the inverse problem to be solved without explicit computation of the sensitivity matrix by using exact derivatives of the discrete formulation Haber et al., 2000. Our technique is based on the discretize-then-optimize approach, which discretizes the forward problem first and then uses a deterministic optimization algorithm to solve the inverse problem Gunzburger, 2003. To this end, we require the discretization of the forward problem. Similar to the work of Celia et al., 1990, we use an implicit Euler method in time and finite volume in space. Given the discrete form, we show that we can analytically compute the derivatives of the forward problem with respect to distributed hydraulic parameters and, as a result, obtain an implicit formula for the sensitivity. The formula involves the solution of a linear time-dependent problem; we avoid computing and storing the sensitivity matrix directly and, rather, suggest a method to efficiently compute the product of the sensitivity matrix and its adjoint times a vector. Equipped with this formulation, we can use a standard inexact Gauss-Newton method to solve the inverse problem for distributed hydraulic parameters in 3D. This large-scale distributed parameter estimation becomes computationally tractable with the technique presented in this chapter and can be employed with any iterative Gauss-Newton-like optimization technique.
This chapter is structured as follows: in Section 3.2, we discuss the discretization of the forward problem on a staggered mesh in space and backward Euler in time; in Section 3.3, we formulate the inverse problem and construct the implicit functions used for computations of the Jacobian-vector product. In Section 3.4.1, we demonstrate the validity of the implementation of the forward problem and sensitivity calculation. In Section 3.4, we validate the numerical implementation and compare to the literature. Chapter \ref{ch:applications} will expand upon the techniques introduced in this chapter to show the effectiveness of the implicit sensitivity algorithm in comparison to existing numerical techniques.
3.1.1Attribution and dissemination¶
To accelerate both the development and dissemination of this approach, we have built these tools on top of an open source framework for organizing simulation and inverse problems in geophysics Cockett et al., 2015. We have released our numerical implementation under the permissive MIT license. Our implementation of the implicit sensitivity calculation for the Richards equation and associated inversion implementation is provided and tested to support 1D, 2D, and 3D forward and inverse simulations with respect to custom empirical relations and sensitivity to parameters within these functions. The source code can be found at https://
3.2Forward problem¶
In this section, we describe the Richards equations and its discretization Richards, 1931. The Richards equation is a nonlinear parabolic partial differential equation (PDE) and we follow the so-called mixed formulation presented in Celia et al., 1990 with some modifications. In the derivation of the discretization, we give special attention to the details used to efficiently calculate the effect of the sensitivity on a vector, which is needed in any derivative based optimization algorithm.
3.2.1Richards equation¶
The parameters that control groundwater flow depend on the effective saturation of the media, which leads to a nonlinear problem. The groundwater flow equation has a diffusion term and an advection term which is related to gravity and only acts in the -direction. There are two different forms of the Richards equation; they differ in how they deal with the nonlinearity in the time-stepping term. Here, we use the most fundamental form, referred to as the 'mixed'-form of the Richards equation Celia et al., 1990:
where is pressure head, is volumetric water content, and is hydraulic conductivity. This formulation of the Richards equation is called the 'mixed'-form because the equation is parameterized in but the time-stepping is in terms of . The hydraulic conductivity, , is a heterogeneous and potentially anisotropic function that is assumed to be known when solving the forward problem. In this chapter, we assume that is isotropic, but the extension to anisotropy is straightforward Cockett et al., 2015Cockett et al., 2016. The equation is solved in a domain, , equipped with boundary conditions on and initial conditions, which are problem-dependent.
An important aspect of unsaturated flow is noticing that both water content, , and hydraulic conductivity, , are functions of pressure head, . There are many empirical relations used to relate these parameters, including the Brooks-Corey model Brooks & Corey, 1964 and the van Genuchten-Mualem model Mualem, 1976Genuchten, 1980. The van Genuchten model is written as:
where
Here, and are the residual and saturated water contents, is the saturated hydraulic conductivity, and are fitting parameters, and, is the effective saturation. The pore connectivity parameter, , is often taken to be , as determined by Mualem (1976). Figure 3.1 shows the functions over a range of negative pressure head values for four soil types (sand, loam, sandy clay, and clay). The pressure head varies over the domain . When the value is close to zero (the left hand side), the soil behaves most like a saturated soil where and . As the pressure head becomes more negative, the soil begins to dry, which the water retention curve shows as the function moving towards the residual water content (). Small changes in pressure head can change the hydraulic conductivity by several orders of magnitude; as such, is a highly nonlinear function, making the Richards equation a nonlinear PDE.
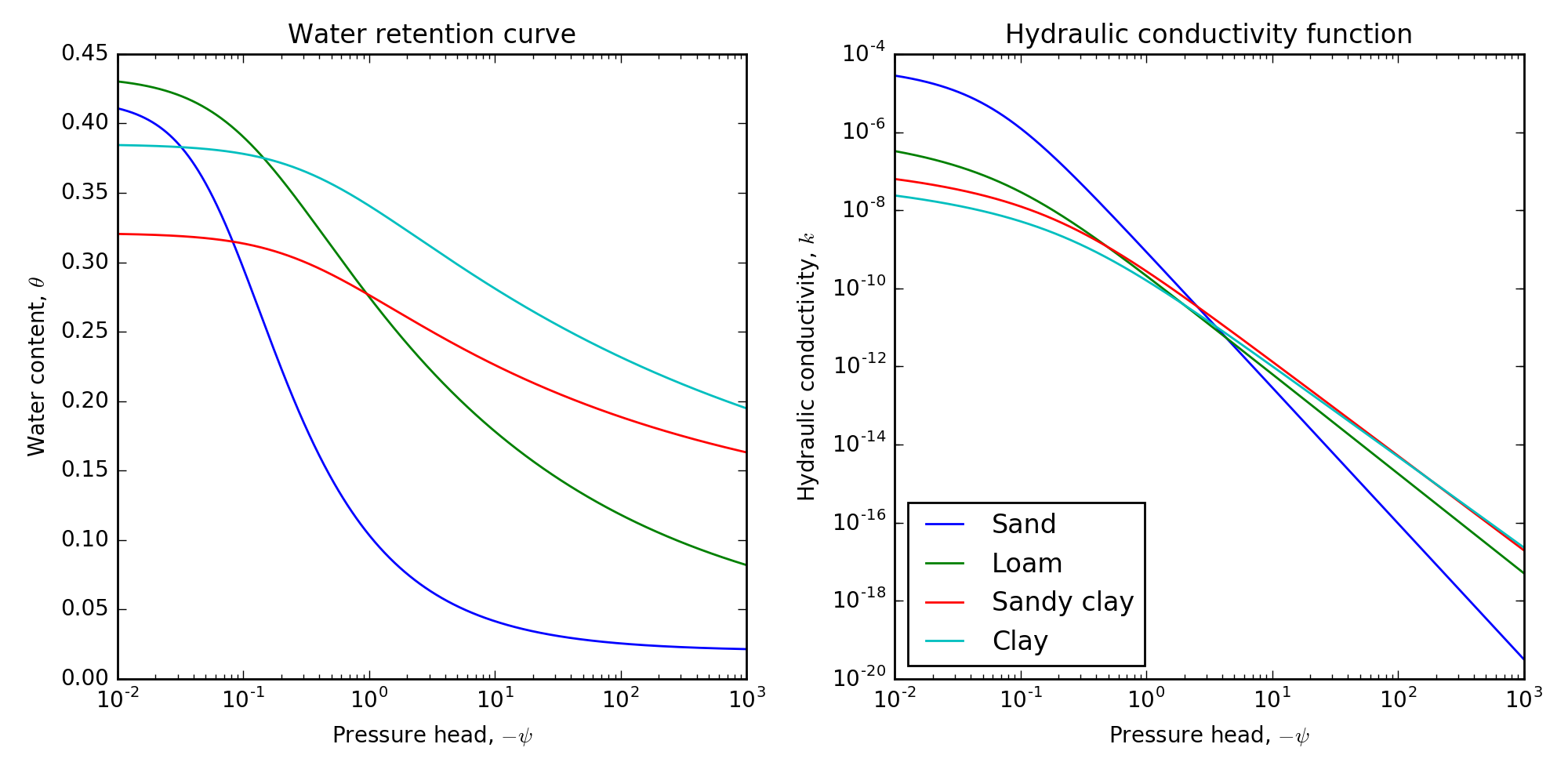
Figure 3.1:The water retention curve and the hydraulic conductivity function for four canonical soil types of sand, loam, sandy clay, and clay.
3.2.2Discretization¶
The Richards equation is parameterized in terms of pressure head, . Here, we describe simulating the Richards equation in one, two, and three dimensions. We start by discretizing in space and then we discretize in time. This process yields a discrete, nonlinear system of equations; for its solution, we discuss a variation of Newton's method.
Spatial Discretization¶
In order to conservatively discretize the Richards equation, we introduce the flux and rewrite the equation as a first order system of the form:
We then discretize the system using a standard staggered finite volume discretization (cf. Ascher (2008)Haber (2015)Cockett et al. (2016), and Appendix \ref{ch:discretize}). This discretization is a natural extension of mass-conservation in a volume where the balance of fluxes into and out of a volume are conserved Lipnikov & Misitas, 2013. Here, it is natural to assign the entire cell one hydraulic conductivity value, , which is located at the cell center. Such assigning leads to a piecewise constant approximation for the hydraulic conductivity and allows for discontinuities between adjacent cells. From a geologic perspective, discontinuities are prevalent, as it is possible to have large differences in hydraulic properties between geologic layers in the ground. The pressure head, , is also located at the cell centers and the fluxes are located on cell faces, which lead to the usual staggered mesh or Marker and Cell (MAC) discretization in space Fletcher, 1988. We demonstrate the discretization in 1D, 2D and 3D on the tensor mesh in Figure 3.2. We discretize the function, , on a cell-centered grid, which results in a grid function, . We use bold letters to indicate other grid functions.
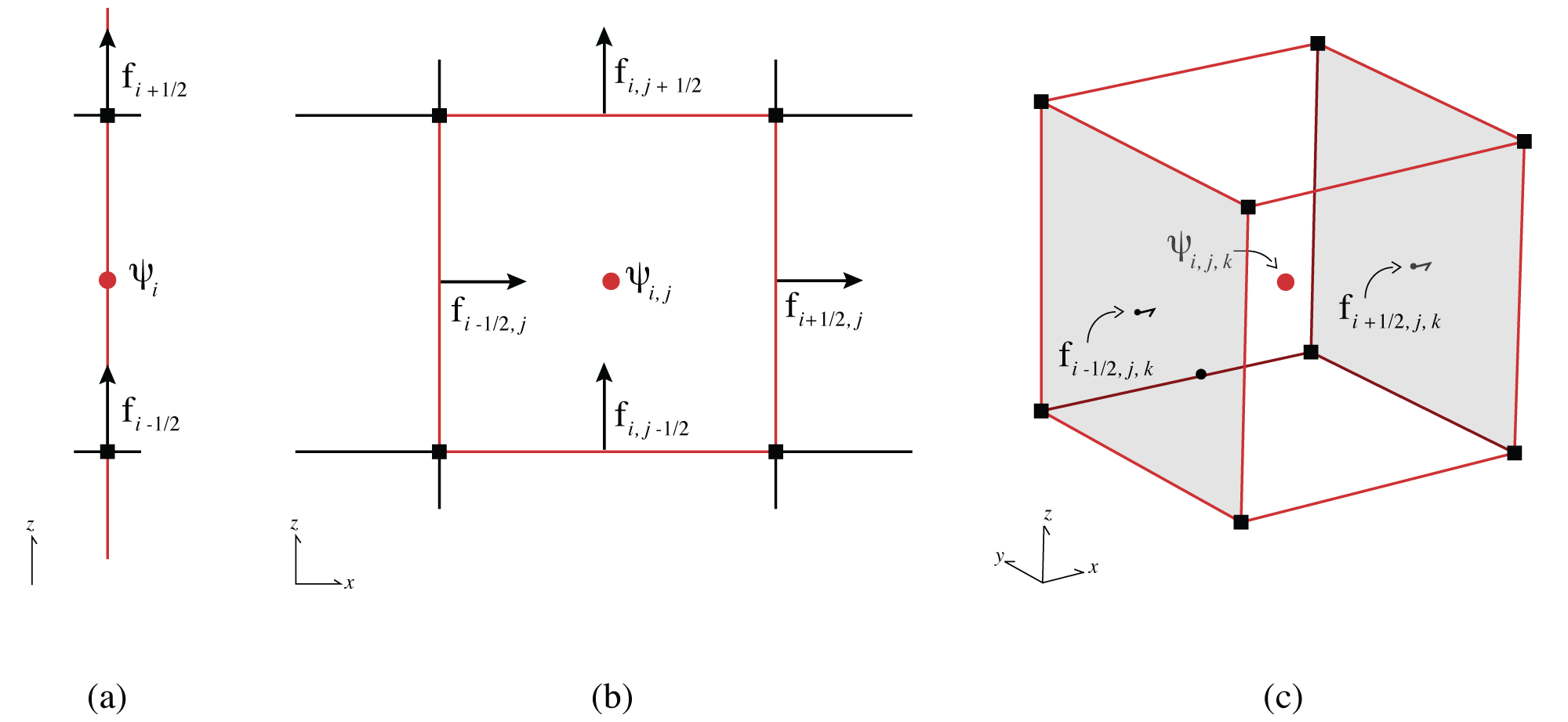
Figure 3.2:Discretization of unknowns in 1D, 2D and 3D space. Red circles are the locations of the discrete hydraulic conductivity and the pressure head . The arrows are the locations of the discretized flux on each cell face. Modified after Cockett et al. (2016).
The discretization of a diffusion-like equation on an orthogonal mesh is well-known (see Haber & Ascher, 2001Fletcher, 1988Haber et al., 2007Ascher & Greif, 2011 and reference within). We discretize the differential operators by using the usual mass balance consideration and the elimination of the flux, [2]. This spatial discretization leads to the following discrete nonlinear system of ordinary differential equations (assuming homogeneous Dirichlet boundary conditions):
Here, is the discrete divergence operator and is the discrete gradient operator. The discrete derivative in the -direction is written as . The values of and are known on the cell-centers and must be averaged to the cell-faces, which we complete through harmonic averaging Haber & Ascher, 2001.
where is a matrix that averages from cell-centers to faces and the division of the vector is done pointwise; that is, we use the vector notation, . We incorporate boundary conditions using a ghost-point outside of the mesh Trottenberg et al., 2001.
Time discretization and stepping¶
The Richards equation is often used to simulate water infiltrating an initially dry soil. At early times in an infiltration experiment, the pressure head, , can be close to discontinuous. These large changes in are also reflected in the nonlinear terms and ; as such, the initial conditions imposed require that an appropriate time discretization be chosen. Hydrogeologists are often interested in the complete evolutionary process, until steady-state is achieved, which may take many time-steps. Here, we describe the implementation of a fully-implicit backward Euler numerical scheme. Higher-order implicit methods are not considered here because the uncertainty associated with boundary conditions and the fitting parameters in the Van Genuchten models (eq. (3.2)) have much more effect than the order of the numerical method used.
The discretized approximation to the mixed-form of the Richards equation, using fully-implicit backward Euler, reads:
This is a nonlinear system of equations for that needs to be solved numerically by some iterative process. Either a Picard iteration (as in Celia et al. (1990)) or a Newton root-finding iteration with a step length control can be used to solve the system. Note that to deal with dependence of with respect to in Newton's method, we require the computation of . We can complete this computation by using the analytic form of the hydraulic conductivity and water content functions (e.g. derivatives of eq. (3.2)). We note that a similar approach can be used for any smooth curve, even when the connection between and are determined empirically (for example, when is given by a spline interpolation of field data).
3.2.3Solving the nonlinear equations¶
Regardless of the empirical relation chosen, we must solve (3.7) using an iterative root-finding technique. Newton's method iterates over until a satisfactory estimation of is obtained. Given , we approximate as:
where the Jacobian for iteration, , is:
The Jacobian is a large dense matrix, and its computation necessitates the computation of the derivatives of . We can use numerical differentiation in order to evaluate the Jacobian (or its product with a vector). However, in the context of the inverse problem, an exact expression is preferred. Given the discrete forward problem, we obtain that:
Here, recall that is harmonically averaged and its derivative can be obtained by the chain rule:
Similarly, for the second term in ((3.10)) we obtain:
Here the notation has been dropped for brevity. For the computations above, we need the derivatives of functions and ; note that, since the relations are assumed local (point wise in space) given the vector, , these derivatives are diagonal matrices. For Newton's method, we solve the linear system:
For small-scale problems, we can solve the linear system using direct methods; however, for large-scale problems, iterative methods are more commonly used. The existence of an advection term in the PDE results in a non-symmetric linear system in the Newton solve. Thus, when using iterative techniques to solve this system, an appropriate iterative method, such as bicgstab or gmres Saad, 1996Barrett et al., 1994, must be used. For a discussion on solver choices in the context of the Richards equation please see Orgogozo et al. (2014).
At this point, it is interesting to note the difference between the Newton iteration and the Picard iteration suggested in Celia et al., 1990. We can verify that the Picard iteration uses an approximation to the Jacobian given by dropping the second term from (3.12). This term can have negative eigenvalues and dropping it is typically done when considering the lagged diffusivity method Vogel, 2001. However, as discussed in Vogel, 2001, ignoring this term can slow convergence.
Finally, a new iterate is computed by adding the Newton update to the last iterate:
where is a parameter that guarantees that
To obtain , we perform an Armijo line search Nocedal & Wright, 1999. In our numerical experiments, we have found that this method can fail when the hydraulic conductivity is strongly discontinuous and changes rapidly. In such cases, Newton's method yields a poor descent direction. Therefore, if the Newton iteration fails to converge to a solution, the update is performed with the mixed-form Picard iteration. Note that Picard iteration can be used, even when Newton’s method fails, because Picard iteration always yields a descent direction Vogel, 2001.
At this point, we have discretized the Richards equation in both time and space while devoting special attention to the derivatives necessary in Newton's method and the Picard iteration as described in Celia et al., 1990. The exact derivatives of the discrete problem will be used in the following two sections, which outline the implicit formula for the sensitivity and its incorporation into a general inversion algorithm. The implementation is provided as a part of the open source SimPEG project (Cockett et al. (2015), https://simpeg.xyz).
3.3Inverse Problem¶
The location and spatial variability of, for example, an infiltration front over time is inherently dependent on the hydraulic properties of the soil column. As such, direct or proxy measurements of the water content or pressure head at various depths along a soil profile contain information about the soil properties. We pose the inverse problem, which is the estimation of distributed hydraulic parameters, given either water content or pressure data. We frame this problem under the assumption that we wish to estimate hundreds of thousands to millions of distributed model parameters. Due to the large number of model parameters that we aim to estimate in this inverse problem, Bayesian techniques or external numerical differentiation, such as the popular PEST toolbox Doherty, 2004, are not computationally feasible. Instead, we will employ a direct method by calculating the exact derivatives of the discrete the Richards equation and solving the sensitivity implicitly. For brevity, we show the derivation of the sensitivity for an inversion model of only saturated hydraulic conductivity, , from pressure head data, . This derivation can be readily extended to include the use of water content data and inverted for other distributed parameters in the heterogeneous hydraulic conductivity function. We will demonstrate the sensitivity calculation for multiple distributed parameters in the numerical examples (Section 4.5).
The Richards equation simulation produces a pressure head field at all points in space as well as through time. Data can be predicted, , from these fields and compared to observed data, . To be more specific, we let be the (discrete) pressure field for all space and time steps. When measuring pressure head recorded only in specific locations and times, we define the predicted data, , as . Here, the vector is the vector containing all of the parameters which we are inverting for (e.g. , or when using the van Genuchten empirical relation). The matrix, , interpolates the pressure head field, , to the locations and times of the measurements. Since we are using a simple finite volume approach and backward Euler in time, we use linear interpolation in both space and time to compute from . Thus, the entries of the matrix contain the interpolation weights. For linear interpolation in 3D, is a sparse matrix that contains up to eight non-zero entries in each row. Note that the time and location of the data measurement is independent and decoupled from the numerical discretization used in the forward problem. A water retention curve, such as the van Genuchten model, can be used for computation of predicted water content data, which requires another nonlinear transformation, . Note here that the transformation to water content data, in general, depends on the model to be estimated in the inversion, which will be addressed in the numerical examples. For brevity in the derivation that follows, we will make two simplifying assumptions: (1) that the data are pressure head measurements, which requires a linear interpolation that is not dependent on the model; and, (2) that the model vector, , describes only distributed saturated hydraulic conductivity. Our software implementation does not make these assumptions; our numerical examples will use water content data, a variety of empirical relations, and calculate the sensitivity to multiple heterogeneous empirical parameters.
We can now formulate the discrete inverse problem to estimate saturated hydraulic conductivity, , from the observed pressure head data, . We frame the inversion as an optimization problem, which minimizes a data misfit and a regularization term. Chapter \ref{ch:framework} showed an approach for geophysical inversions where hundreds of thousands to millions of distributed parameters are commonly estimated in a deterministic inversion Tikhonov & Arsenin, 1977Oldenburg & Li, 2005Constable et al., 1987Haber, 2015. Please refer to the previous chapter for the details of this inversion methodology. The hydrogeologic literature also shows the use of these techniques; however, there is also a large community advancing stochastic inversion techniques and geologic realism (cf. Linde et al. (2015)). Regardless of the inversion algorithm used, an efficient method to calculate the sensitivity is crucial; this method is the focus of our work.
3.3.1Implicit sensitivity calculation¶
The optimization problem requires the derivative of the pressure head with respect to the model parameters, . We can obtain an approximation of the sensitivity matrix through a finite difference method on the forward problem Šimunek & Genuchten, 1996Finsterle & Kowalsky, 2011Finsterle & Zhang, 2011. One forward problem, or two, when using central differences, must be completed for each column in the Jacobian at every iteration of the optimization algorithm. This style of differentiation proves advantageous in that it can be applied to any forward problem; however, it is highly inefficient and introduces errors into the inversion that may slow the convergence of the scheme Doherty, 2004. Automatic differentiation (AD) can also be used Nocedal & Wright, 1999. However, AD does not take the structure of the problem into consideration and often requires that the dense Jacobian be explicitly formed. Bitterlich & Knabner (2002) presents three algorithms (finite difference, adjoint, and direct) to directly compute the elements of the dense sensitivity matrix for the Richards equation. As problem size increases, the memory required to store this dense matrix often becomes a practical computational limitation Haber et al., 2004Towara et al., 2015. As we show next, it is possible to explicitly write the derivatives of the Jacobian and evaluate their products with vectors using only sparse matrix operations. This algorithm is much more efficient than finite differencing, especially for large-scale simulations, since it does not require explicitly forming and storing a large dense matrix. Rather, the algorithm efficiently computes matrix-vector and adjoint matrix-vector products with sensitivity. We can use these products for the solution of the Gauss-Newton system when using the conjugate gradient method, which bypasses the need for the direct calculation of the sensitivity matrix and makes solving large-scale inverse problems possible. Other geophysical inverse problems have used this idea extensively, especially in large-scale electromagnetics (cf. Haber et al. (2000)). The challenge in both the derivation and implementation for the Richards equation lies in differentiating the nonlinear time-dependent forward simulation with respect to multiple distributed hydraulic parameters.
The approach to implicitly constructing the derivative of the Richards equation in time involves writing the whole time-stepping process as a block bi-diagonal matrix system. The discrete Richards equation can be written as a function of the model. For a single time-step, the equation is written:
In this case, is a vector that contains all the parameters of interest. Note that and are also functions of . In general, and are also dependent on the model; however, for brevity, we will omit these derivatives. The derivatives of to the change in the parameters can be written as:
or, in more detail:
The above equation is a linear system of equations and, to solve for , we rearrange the block-matrix equation:
Here, we use the subscript notation of and to represent two block-diagonals of the large sparse matrix . Note that all of the terms in these matrices are already evaluated when computing the Jacobian of the Richards equations in Section 3.2 and that they contain only basic sparse linear algebra manipulations without the inversion of any matrix. If does not depend on the model, meaning the initial conditions are independent, then we can formulate the block system as:
This is a block matrix equation; both the storage and solve will be expensive if it is explicitly computed. Indeed, its direct computation is equivalent to the adjoint method Bitterlich & Knabner, 2002Oliver & Chen, 2011.
Since only matrix vector products are needed for the inexact Gauss-Newton optimization method, the matrix is never needed explicitly and only the products of the form and are needed for arbitrary vectors and . Projecting the full sensitivity matrix onto the data-space using results in the following equations for the Jacobian:
In these equations, we are careful to not write , as it is a large dense matrix which we do not want to explicitly compute or store. Additionally, the matrices and do not even need to be explicitly formed because the matrix is a triangular block-system, which we can solve using forward or backward substitution with only one block-row being solved at a time (this is equivalent to a single time step). To compute the matrix vector product, , we use a simple algorithm:
- Given the vector calculate
- Solve the linear system for the vector
- Set
Here, we note that we complete steps (1) and (2) using a for-loop with only one block-row being computed and stored at a time. As such, only the full solution, , is stored and all other block-entries may be computed as needed. There is a complication here if data is in terms of water content or effective saturation, as the data projection is no longer linear and may have model dependence. These complications can be dealt with using the chain rule during step (3). Similarly, to compute the adjoint involves the intermediate solve for in and then computation of . Again, we solve the block-matrix via backward substitution with all block matrix entries being computed as needed. Note that the backward substitution algorithm can be viewed as time stepping, which means that it moves from the final time back to the initial time. This time stepping is equivalent to the adjoint method that is discussed in Oliver & Chen (2011) and references within. The main difference between our approach and the classical adjoint-based method is that our approach yields the exact gradient of the discrete system; no such guarantee is given for adjoint-based methods.
The above algorithm and the computations of all of the different derivatives summarizes the technical details of the computations of the sensitivities. Equipped with this "machinery", we now demonstrate that validity of our implementation.
3.4Numerical results¶
The focus of this section is to validate and compare our algorithm and implementation to the literature. The following chapter will focus on applications of this work as well as demonstrate computational scalability of the algorithm for realistic field examples (Chapter \ref{ch:applications}).
3.4.1Validation¶
Forward problem¶
The Richards equation has no analytic solution, which makes testing the code more involved. Here we have chosen to use a fictitious source experiment to rigorously test the code. In this experiment, we approximate an infiltration front by an arctangent function in one dimension, which is centered over the highly nonlinear part of the van Genuchten curves, with centimeters. The arctangent curve advects into the soil column with time. The advantage of using an analytic function is that the derivative is known explicitly and can be calculated at all times. However, it should be noted that the Richards equation does not satisfy the analytic solution exactly, but differs by a function, . We refer to this function as the fictitious source term. The analytic function that we used has similar boundary conditions and shape to an example in Celia et al. (1990) and is considered over the domain .
This analytic function is shown at times 0 and 0.5 in Figure 3.3 and has a pressure head range of . We can compare these values to the van Genuchten curves in Figure 3.1. We can then put the known pressure head into the Richards equation (3.1) and calculate the analytic derivatives and equate them to a source term, . Knowing this source term and the analytic boundary conditions, we can solve discretized form of the Richards equation, which should reproduce the analytic function in Equation (3.23). Table 3.1 shows the results of the fictitious source test when the number of mesh-cells is doubled and the time-discretization is both fixed and equivalent to the mesh size (i.e. ). In this case, we expect that the backward-Euler time discretization, which is , will limit the order of accuracy. The final column of Table 3.1 indeed shows that the order of accuracy is . The higher errors in the coarse discretization are due to high discontinuities and changes in the source term, which the coarse discretization does not resolve. We can complete a similar procedure in two and three dimensions and these tests show similar results of convergence. The rigorous testing of the code presented provides confidence in the forward simulation that is used throughout the following sections of this chapter.
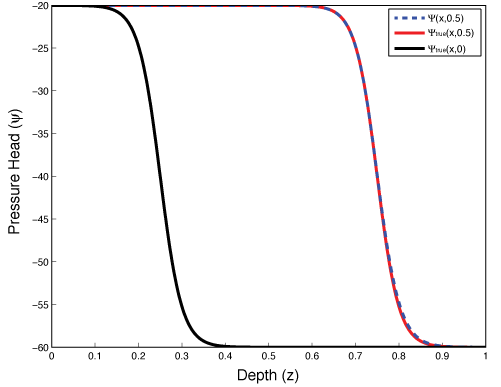
Figure 3.3:Fictitious source test in 1D showing the analytic function at times 0.0 and 0.5 and the numerical solution using the mixed-form Newton iteration.
Table 3.1:Fictitious source test for Richards equation in 1D using the mixed-form Newton iteration.
| Mesh Size (n) | Order Decrease, | |
|---|---|---|
| 64 | 5.485569e+00 | - |
| 128 | 2.952912e+00 | 0.894 |
| 256 | 1.556827e+00 | 0.924 |
| 512 | 8.035072e-01 | 0.954 |
| 1024 | 4.086729e-01 | 0.975 |
| 2048 | 2.060448e-01 | 0.988 |
| 4096 | 1.034566e-01 | 0.994 |
| 8192 | 5.184507e-02 | 0.997 |
Inverse problem¶
In order to test the implicit sensitivity calculation, we employ derivative and adjoint tests as described in Haber (2015). Given that the Taylor expansion of a function is
for any of the model parameters considered, we see that our approximation of by should converge as as is reduced. This allows us to verify our calculation of . To verify the adjoint, , we check that
for any two random vectors, and . These tests are run for all of the parameters considered in an inversion of the Richards equation. Within our implementation, both the derivative and adjoint tests are included as unit tests which are run on any updates to the implementation (https://
3.4.2Comparison to literature¶
Code-to-code comparisons have been completed for comparison to Celia et al. (1990), which can be found in Cockett (2017). The following results are a direct comparison to the results produced by Celia et al. (1990) for the Picard iteration only; Celia et al. (1990) did not implement the Newton iteration. The direct comparison is completed: (a) to give confidence to the numerical results; (b) to compare the Newton iteration to the Picard iteration of the mixed formulation for a well-known example; and (c) demonstrate the use of multiple empirical models. Here, we use the Haverkamp model Haverkamp et al., 1977 (rather than the classically used van Genuchten model) for the water retention and hydraulic conductivity functions.
We used parameters of , , , , , , and m/s, which are the same as in Celia et al. (1990). The 40 cm high 1D soil column has initially dry conditions with a pressure head cm. The boundary conditions applied are inhomogeneous Dirichlet with the top of the soil column, cm, and the bottom of the soil column, cm. The initial conditions are not consistent with the boundary condition at the top of the soil profile. This inconsistency leads to a boundary layer and a steep gradient in the pressure head at early times; as such, we anticipate that the Newton iteration will converge slowly at these times. The spatial grid is regular and has a spacing of 1.0cm, while the time-stepping, , is manipulated. The three iterative methods described in Section 3.2 are implemented and compared at 360s: (1) head-based form Picard; (2) mixed-form Picard; and, (3) mixed-form Newton. Figure 3.4 shows the solution obtained with the three iterative methods. Comparing the head-based formulation to the mixed-formulation for a large time-step (e.g. s) shows the degradation of the head-based method. Not only is the infiltration front smoothed, there is underestimate of the front location (Figure 3.4a). The underestimate of the infiltration front location is due to a loss of mass, which can be traced back the initial formulation of the head-based method Celia et al., 1990. The mixed-formulation, solved with either a Picard iteration or a Newton method, conserves mass and correctly identifies the spatial location of the infiltration front (Figure 3.4b). The results obtained here show excellent agreement with Celia et al. (1990).
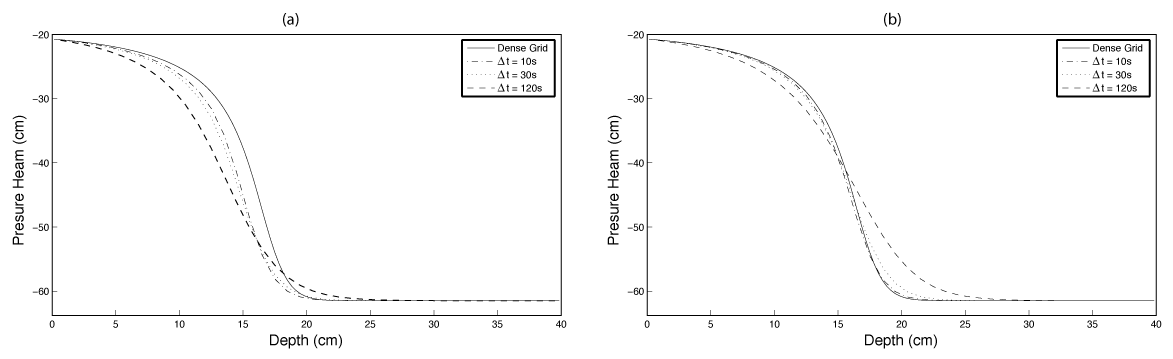
Figure 3.4:Comparison of results to Celia et al. (1990) showing the differences in the (a) head-based and (b) mixed formulations for =360s.
3.5Conclusions¶
The number of parameters that are estimated in the Richards equation inversions has grown and will continue to grow as time-lapse data and geophysical data integration become standard in site characterizations. The increase in data quantity and quality provides the opportunity to estimate spatially distributed hydraulic parameters from the Richards equation; doing so requires efficient simulation and inversion strategies. In this chapter, we have shown a derivative-based optimization algorithm that does not store the Jacobian, but rather computes its effect on a vector (i.e. or ). By not storing the Jacobian, the size of the problem that we can invert becomes much larger. We have presented efficient methods to compute the Jacobian that can be used for all empirical hydraulic parameters, even if the functional relationship between parameters is obtained from laboratory experiments.
Our technique allows a deterministic inversion, which includes regularization, to be formulated and solved for any of the empirical parameters within the Richards equation. For a full 3D simulation, as many as ten spatially distributed parameters may be needed, resulting in a highly non-unique problem; as such, we may not be able to reasonably estimate all hydraulic parameters. Depending on the setting, amount of a-priori knowledge, quality and quantity of data, the selection of which parameters to invert for may vary. Our methodology enables practitioners to experiment in 1D, 2D and 3D with full simulations and inversions, in order to explore the parameters that are important to a particular dataset. Our numerical implementation is provided in an open source repository (https://simpeg.xyz) and is integrated into the framework presented in Chapter \ref{ch:framework}. The goal of Chapter \ref{ch:applications} is to work with these techniques in an experiment that represents a field infiltration experiment. The following chapter will also further document the scalability of this approach when moving to 3D inversions.
- Cockett, R., Heagy, L. J., & Haber, E. (2017). A numerical method for efficient 3D inversions using Richards equation. arXiv.
- Cockett, R., & Haber, E. (2013). Inversion for hydraulic conductivity using the unsaturated flow equations. SIAM Conference on Mathematical & Computational Issues in the Geosciences.
- Cockett, R., & Haber, E. (2013). A Numerical Method for Large Scale Estimation of Distributed Hydraulic Conductivity from Richards Equation. AGU Fall Meeting.
- Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. Journal of Applied Physics, 1(5), 318–333. 10.1063/1.1745010
- Celia, M. A., Bouloutas, E. T., & Zarba, R. L. (1990). A general mass-conservative numerical solution for the unsaturated flow equation. Water Resources Research, 26(7), 1483–1496. 10.1029/WR026i007p01483